El ajuste de riesgo país: ¿Es necesaria su instrumentación?

Los contribuyentes del régimen de precios de transferencia en cumplimiento de sus obligaciones tienen que demostrar que sus operaciones con partes relacionadas fueron pactadas como con terceros independientes en operaciones comparables, es decir, en función del principio arm's length. Para estos efectos deben seleccionar un método de precios de transferencia en atención a la jerarquía establecida en el artículo 180 de la Ley del Impuesto Sobre la Renta (LISR). En México, se ha popularizado el uso de métodos que comparan los márgenes de rentabilidad asociados a las operaciones intercompañía (o en el peor de los casos al contribuyente en global), vs los márgenes de rentabilidad obtenidos por terceros independientes "comparables", que con frecuencia se localizan en países distintos a México. -Esto por la insuficiencia de información pública disponible de compañías mexicanas-. Ante este escenario, las autoridades fiscales mexicanas en seguimiento a recomendaciones previas efectuadas por el toolkit de la plataforma de colaboración conjunta OCDE-ONU-FMI-BM e inclusive retomadas en el cóctel de precios de transferencia del CIAT proponen un "ajuste de riesgo país". Este ajuste "normaliza" la comparación entre empresas mexicanas y extranjeras, a partir una fórmula matemática que corrige la rentabilidad de las compañías extranjeras incorporando el efecto que tendrían de haber operado en México.

La fórmula de ajuste está publicada en la sección de preguntas frecuentes del Servicio de Administración Tributaria como sigue:

Ajuste por riesgo país = Activos operativos promedio de los últimos años de la empresa comparable (localizada en un país desarrollado) × EMBI (emerging market bond index) correspondiente a México)

Aplicación del ajuste

Ventas de la empresa comparable + ajuste por riesgo país

Ante esta postura por parte de las autoridades fiscales, convendría preguntarnos: ¿hay un impacto significativo de la localización geográfica en los márgenes de utilidad de las empresas? y ¿la fórmula propuesta por las autoridades fiscales responde a las exigencias teóricas que le dan lugar?

Para responder a la primera pregunta hay que considerar que la propuesta de ajuste por riesgo país responde a una presunción riesgo- rendimiento. Para este caso concreto dicha presunción implica que las diferencias en localización de las compañías significan la exposición a diferentes niveles de riesgo, y que en respuesta, estas compañías sólo permanecerían en dichos países si perciben una remuneración que compense adecuadamente la exposición al riesgo.

Por tanto, el uso de empresas o transacciones "comparables" ubicadas en distintas localizaciones ameritaría la realización de un ajuste en los márgenes de utilidad a fin de anular el efecto de localización en los márgenes con el propósito de mejorar la comparabilidad entre las transacciones analizadas.

Teniendo en cuenta que los países emergentes son considerados estructuralmente más riesgosos que los desarrollados, la hipótesis de riesgo-rendimiento nos llevaría a plantear que en términos de esta compensación al riesgo, los países emergentes tendrían que ofrecer rendimientos más altos a los obtenidos en las economías desarrolladas.

Para evaluar si existe estadísticamente diferencia de rendimientos entre países emergentes y desarrollados se propuso al interior de nuestra firma un análisis comparativo de los rendimientos obtenidos por empresas localizadas tanto en países emergentes como en países desarrollados a partir del siguiente procedimiento:

Para el análisis comparativo inicial, se instrumentó una búsqueda en la base de datos BvD Osiris (actualizada a marzo de 2019) a partir de los siguientes parámetros:

• Empresas activas.

• Empresas con cuentas del año 2018.

• Empresas que cotizan en bolsa.

• Empresas con página web.

• Empresas con dato disponible de utilidad bruta/costo de ventas (C⁺).

• Empresas con dato disponible de margen operativo (MO).

• Empresas localizadas en los siguientes países:

• Países desarrollados: Australia, Austria, Alemania, Bélgica, Canadá, Corea de Sur, Dinamarca, España, Estados Unidos, Finlandia, Francia, Irlanda, Italia, Japón, Noruega, Nueva Zelanda, Portugal, Reino Unido, Singapur, Suecia y Suiza.

• Países emergentes: Brasil, Chile, China, Colombia, Egipto, Filipinas, Grecia, Hungría, India, Indonesia, Malasia, Marruecos, México, Perú, Polonia, Rusia, Sudáfrica, Tailandia, Taiwán y Turquía.

De la selección anterior se obtiene una muestra de 7,609 empresas.

Dado que el propósito es evaluar la diferencia de los márgenes de utilidad entre las empresas de países emergentes respecto de los países desarrollados en cada industria, las empresas se clasificaron por grupo mayor (Major Group acorde a los dos primeros dígitos del SIC US) y de estas sub-industrias sólo se utilizaron aquellas con por lo menos 10 observaciones de empresas en países emergentes y desarrollados respectivamente, dándonos como resultado 45 sub-industrias a evaluar y reduciendo la muestra de 7,609 empresas a 7,065.

Además, el análisis se realizará en función de dos ratios distintos, los cuales son: Utilidad bruta/costo de ventas (C⁺) y margen operativo (MO), para confirmar la veracidad de la prueba a partir del uso de distintos indicadores financieros.

Resumiendo lo visto anteriormente, la hipótesis que nos interesa evaluar es si los márgenes de utilidad de las empresas en países emergentes se diferencian significativamente de los márgenes obtenidos en los países desarrollados. En este caso se realiza la prueba Kolmogorov-Smirnov para averiguar si la distribución de probabilidad de los márgenes en ambos grupos es distinta para cada sub-industria.

Sea F_n(x) la función de probabilidad acumulada definida como:

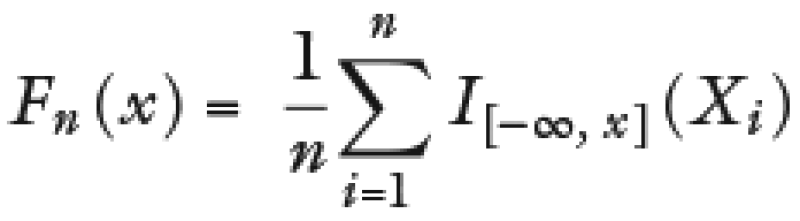
Donde I_{[–∞, x]}(X_i) es la función indicadora, igual a 1 sí X_i ⩽ x e igual a 0 en otro caso, el estadístico Kolmogorov-Smirnov es el siguiente:

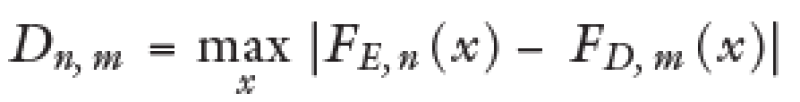
Donde F_E,n y F_D,m(x) son las funciones de probabilidad acumulada de las dos muestras que corresponden al grupo de empresas en países emergentes y al grupo de empresas en países desarrollados respectivamente.

La hipótesis nula indica que ambas muestras presentan la misma distribución y se rechaza si se cumple que:

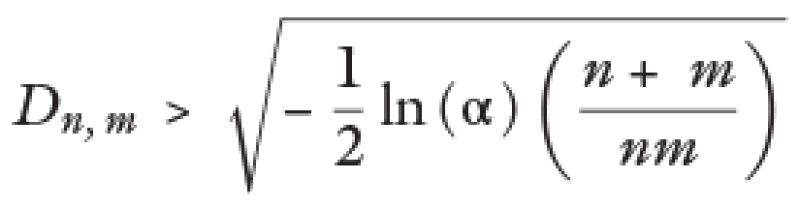
Donde α corresponde al nivel de confianza (1–α)%.

Tabla 1. Resultados de prueba Kolmogorov-Smirnov
	C+	MO
US SIC donde se acepta la hipótesis nula.	01, 10, 13, 15, 17, 20, 22, 23, 24, 25, 26, 27, 29, 30, 34, 35, 37, 38, 39, 42, 44, 45, 48, 49, 50, 53, 57, 58, 59, 60, 62, 65, 70, 73, 79, 80	01, 10, 13, 15, 17, 20, 22, 23, 24, 25, 26, 27, 29, 30, 34, 35, 37, 38, 39, 42, 44, 45, 48, 49, 50, 53,  57, 58, 59, 60, 62, 65, 70, 73, 79, 80
US SIC donde se rechaza la hipótesis nula.	16, 28, 32, 33, 36, 47, 51, 67, 87	16, 28, 32, 33, 36, 47, 51, 67, 87
Fuente: BvD Osiris. US SIC: indica los dos primeros dígitos del código SIC US al que corresponden las empresas incluidas en la prueba Kolmogorov-Smirnov.

En la Tabla 1 se presentan los resultados sobre los datos de la base de datos, donde podemos apreciar que en el caso de ambos ratios, sólo en 9 de las 45 sub-industrias analizadas se reporta que la prueba Kolmogorov-Smirnov arroja el rechazo de la hipótesis nula. Es decir, los resultados indican que estamos lejanos a observar de forma generalizada o consistente una diferencia entre la distribución de los márgenes de los países emergentes y los países desarrollados.

Respecto a la segunda interrogante, cabe recordar que específicamente la hipótesis de riesgo-rendimiento se refiere a una relación positiva entre el rendimiento esperado (no el que se termine logrando finalmente) con el riesgo o incertidumbre de lograr este mismo rendimiento esperado. Pues los agentes económicos preferirán definitivamente un activo con rendimiento esperado más alto que otro cuando ambos tienen el mismo nivel de riesgo y también preferirían un activo con menor riesgo que otro cuando ambos tienen el mismo rendimiento esperado.

En consecuencia, solo "sobrevivirán" en el mercado activos que guarden entre sí una relación de compensación entre riesgo y rendimiento.

Las métricas más comunes para referirse al rendimiento esperado es la media, mientras que en el caso del riesgo la medida más común es la varianza, la cual nos indica el nivel de volatilidad.

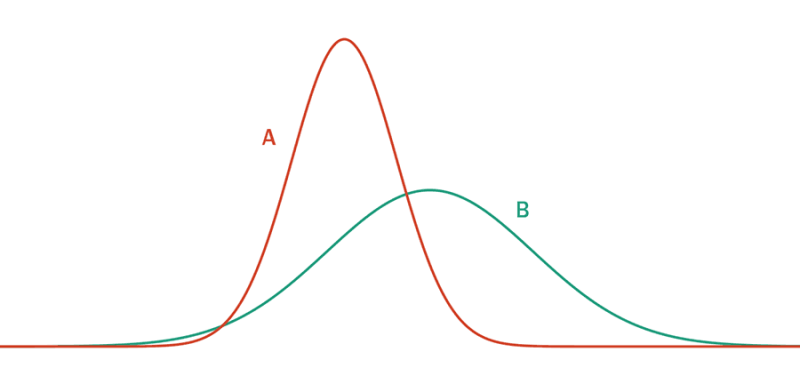
Siendo así, a continuación se muestra gráficamente (Gráfica 1) dos distribuciones correspondientes a activos diferentes (A y B) donde: La función de distribución el activo A tiene una media mayor a la de la función de distribución del activo B y la varianza de la distribución A también es mayor a la varianza de la distribución B, haciendo notar la relación positiva a mantener entre riesgo y rendimiento entre activos que permanecen en el mercado.

Por otro lado, al margen de la discusión sobre si el ajuste de riesgo país debe realizarse o no, es de sumo interés revisar si la forma de realizar el ajuste cumple con las características necesarias para hacer prevalecer de manera completa la hipótesis riesgo-rendimiento, que es el concepto teórico sobre el cual se sostiene la postura de la necesidad de su implementación.

A continuación, se presenta un caso específico en el que evaluaremos si esta fórmula de ajuste por riesgo país sugerida por las autoridades logra cumplir con las propiedades de la hipótesis riesgo-rendimiento que describimos anteriormente.

Supongamos que respecto a C⁺ tenemos n empresas comparables del país A (país desarrollado) y la empresa analizada está en México (país B). El país A es menos riesgoso que el país B, dicho de otra manera, tendríamos observaciones de comparables que corresponden a la distribución A de la Gráfica 1 y con el ajuste buscamos transformarlas a la distribución B (correspondiente a un país más riesgoso) a través de la fórmula de ajuste.

En este caso, si la fórmula de ajuste por riesgo país es correcta, al aplicar el ajuste se debe presentar un incremento en la media y varianza de los márgenes de utilidad de estas empresas comparables.

Formula C⁺ antes de ajuste (V = ventas, CV = costo de ventas):

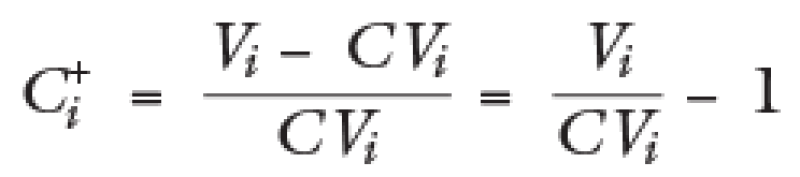
Formula C⁺ después de ajuste (RP_aji = ajuste de riesgo país para la comparable i):

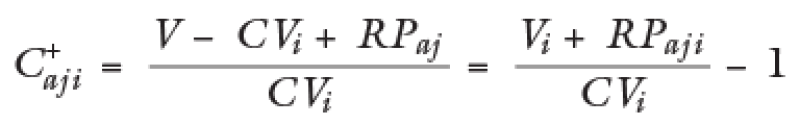
Formula de la media de C⁺ antes de ajuste:

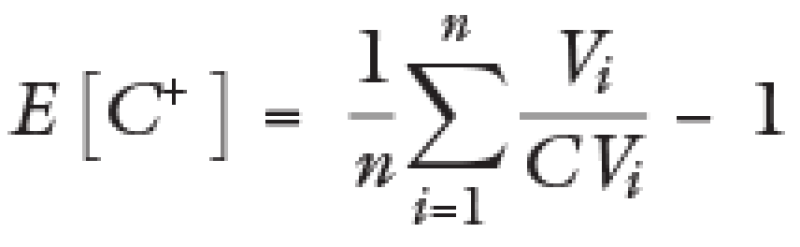
Formula de la media de C⁺ después de ajuste:

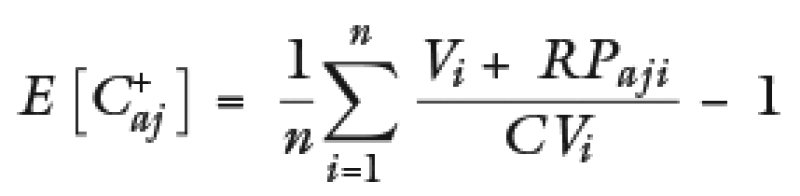
Tal que en este caso RP_aji > 0 para todo i.

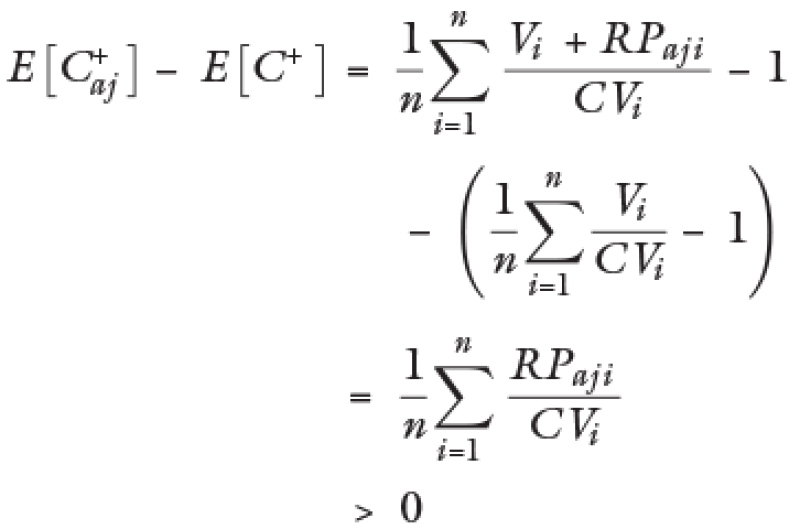
Es decir, cumple con el principio de incrementar en la media de C⁺ al realizar el ajuste con la fórmula que estamos analizando. Ahora procedemos a evaluar el efecto en la varianza.

Formula de la varianza del C⁺ antes de ajuste:

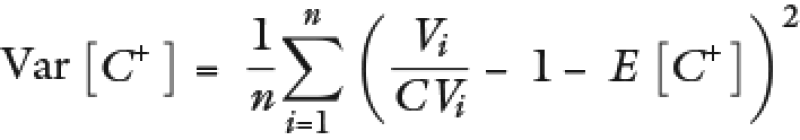
Formula de la varianza después de ajuste:

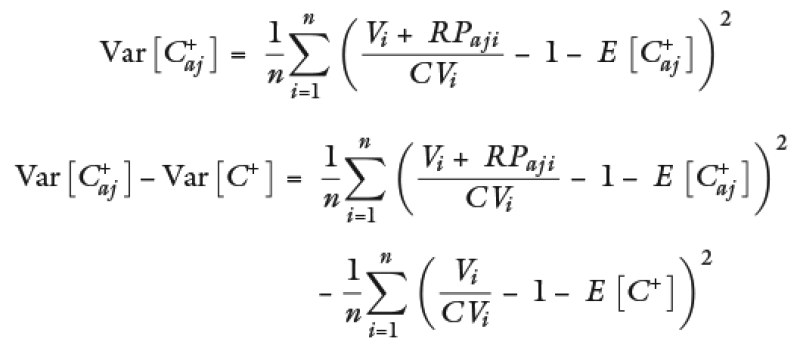
Sustituyendo

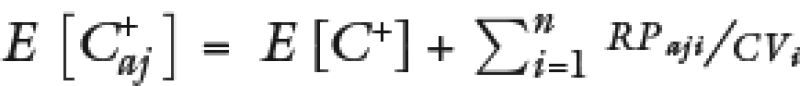
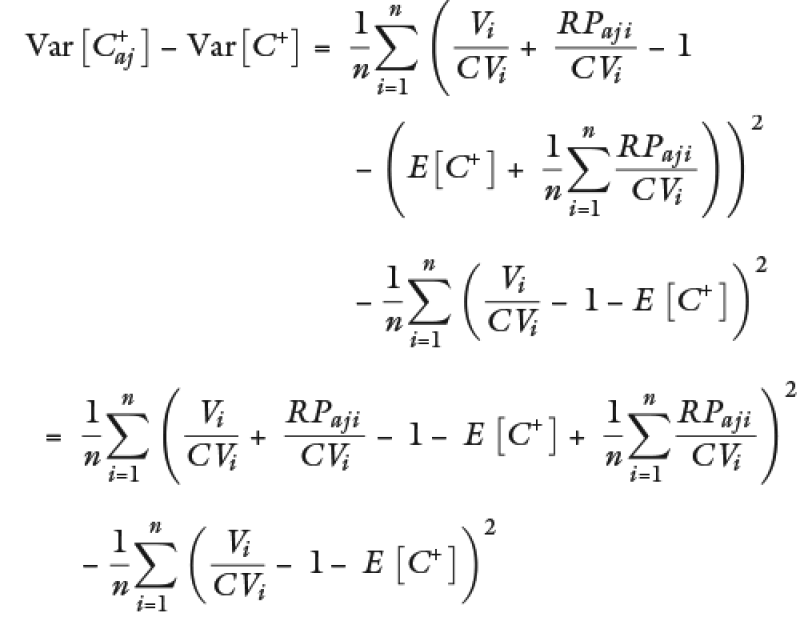
Sustituyendo

y.

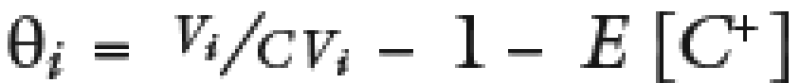
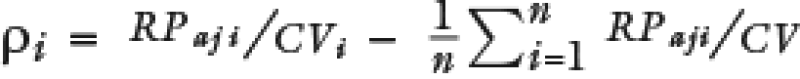
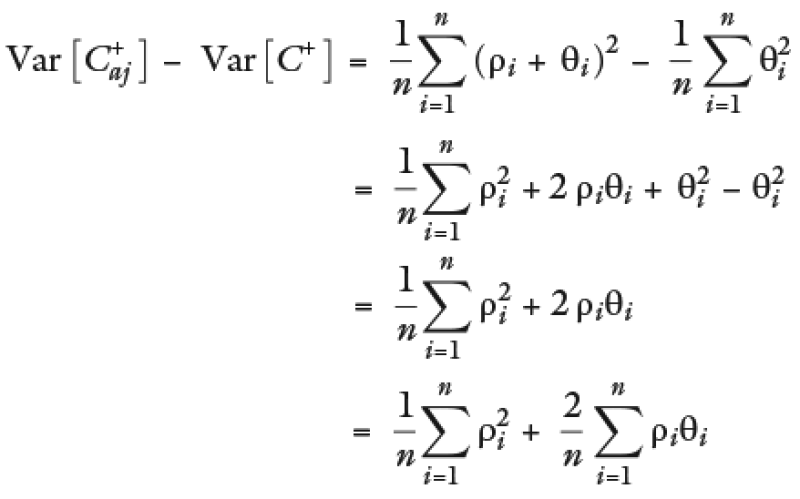
Sustituyendo ρ_i y θ_i

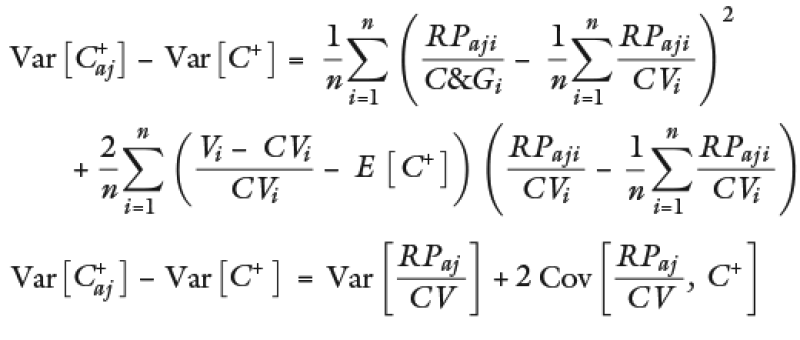
Tal que no puede asegurarse que

en todos los casos se cumpliría que entonces no se puede asegurar que

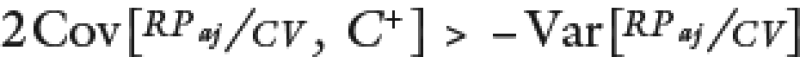
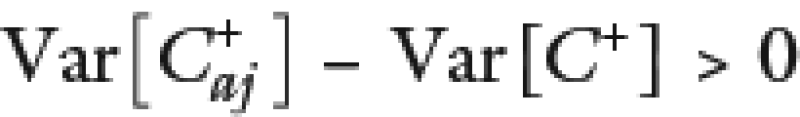
Es decir, el efecto en la varianza al realizar el ajuste resulta indeterminado a diferencia de la media, que como vimos anteriormente, el ajuste la aumenta con absoluta certeza.

En conclusión, la fórmula de ajuste propuesta lograría incrementar la media de la distribución (valor esperado de los márgenes) de los márgenes pero no necesariamente el incremento de la varianza que debería tener (volatilidad de los márgenes) para hacer cumplir la hipótesis riesgo-rendimiento.

Hay que recordar que la hipótesis riesgo – rendimiento supone una compensación a la incertidumbre de efectivamente obtener ese mismo rendimiento esperado. En consecuencia, no es del todo correcto realizar un ajuste desde la perspectiva de "sumar" una utilidad adicional en función de algún spread de activos financieros que coticen del país de la empresa analizada y del país de la empresa comparable como si tuviésemos certeza de que ese rendimiento adicional se logrará, pues es de hecho, esa diferencia un signo de que existen distintos niveles de certidumbre entre el rendimiento esperado y el que finalmente se logre en cada país.

Es de suma importancia, que en el marco de la hipótesis de riesgo-rendimiento trasladada concretamente a las medidas de media y varianza de las distribuciones de los márgenes de utilidad, se apliquen alternativas de ajuste que hagan cumplir los fundamentos de dichos aspectos teóricos en las distribuciones de los márgenes ajustados que finalmente repercutirán en el cambio de los rangos intercuartilicos cuando se realiza un ajuste de riesgo país.

Como se puede apreciar, del análisis instrumentado y a partir de los datos considerados se puede concluir que: i) no existe evidencia estadística que demuestre una correlación positiva entre localización y rendimiento y ii) la fórmula matemática empleada para el ajuste no se alinea a los supuestos teórico económicos en los que descansa su presunta aplicación. Adicionalmente debe considerarse que la instrumentación del ajuste de riesgo país eliminaría los location savings de operar en México. Es decir, si un grupo multinacional decide instalar una subsidiaria en el país en consideración a sus ventajas competitivas, por ejemplo, un menor costo de mano de obra, la instrumentación del ajuste tendería a eliminar esa ventaja competitiva al incrementar la rentabilidad del contribuyente mexicano hasta los niveles obtenidos por empresas o transacciones localizadas en países desarrollados. Eso, en las circunstancias actuales, sería un tiro en el pie para la administración fiscal justo cuando en vista de la contracción del PIB el país requiere precisamente lo contrario, incrementar la inversión extranjera aprovechando el apetito de los grupos multinacionales por salir de China, un competidor directo de México en el sector de manufactura.

Desde luego, no debe demeritarse el problema de la falta de datos suficientes para instrumentar análisis de comparabilidad apropiados, pero debe insistirse en el uso de comparables internos, la adecuada selección de mercados de los comparables (inclusive y en su caso considerando sets regionales), o inclusive considerar seleccionar a la contraparte en la operación como entidad analizada, cuando así lo permitan las circunstancias. Como corolario, sobra decir que el contribuyente debe comprender los supuestos en los que descansa su análisis y la selección de comparables, porque una selección inadecuada puede conducir a correcciones por demás gravosas por parte de las autoridades fiscales.

Click here to read this article in English

Click here to read the entire 2020 Mexico Special Focus guide

Jesús Aldrin Rojas

Socio Director QCG Transfer Pricing Practice T: +52 55 5395 1968 E: jesus.aldrin.rojas@qcglatam.com Jesús Aldrin Rojas es licenciado en contaduría por la UNAM, MBA por el ITAM, y MGM por la Universidad de Tulane. Es coordinador nacional del Comité Fiscal de la Cámara México-Alemana de Comercio e Industria (CAMEXA), profesor de la materia de precios de transferencia en la maestría de impuestos en la Universidad Panamericana y miembro del Comité Técnico Nacional de Precios de Transferencia en el Instituto Mexicano de Ejecutivos de Finanzas (IMEF). Es también el primer perito de precios de transferencia ante el Consejo de la Judicatura Federal en México (P1326.2020). Actualmente asiste a grupos nacionales y multinacionales proveyendo consultoría estratégica en materia de precios de transferencia e impuestos internacionales, principalmente con relación al plan de acción de la OCDE para combatir la evasión fiscal y la transferencia de utilidades (el plan BEPS).

José Augusto Chamorro Gómez

Economista Senior QCG Transfer Pricing Practice T: +52 55 5395 1968 E: jose.chamorro@qcglatam.com José Augusto es licenciado y maestro en ciencias económicas por el Instituto Politécnico Nacional (IPN) y maestro en finanzas por el Instituto Tecnológico Autónomo de México (ITAM) en México. José Augusto asiste a grupos nacionales y multinacionales proveyendo consultoría, desarrollo de políticas de precios de transferencia y soporte en la elaboración de documentación comprobatoria en materia de precios de transferencia en los términos requeridos en la legislación mexicana y la acción 13 de plan BEPS de la OCDE (reporte país a país y documentación de precios de transferencia). José Augusto atiende a clientes en el sector de tecnologías de información, manufactura, y servicios en aspectos como valuación de intangibles, desarrollo de modelos econométricos, instrumentación de procesos de optimización, etc. José es miembro del Colegio Nacional de Economistas y autor regular en publicaciones especializadas en el país.